Focusing chamber theoretical analysis

Note: this is a very old page written way back in 2023. Since then, we’ve actually realized that this is all completely wrong. The math is correct, the physics isn’t, and geometric methods, while suitable in optics, does not work very well in the microwave regime.

However, this page has historical significance in that it was written very shortly after the Project Elara team was formed at RPI (in September of 2023); previously, Project Elara was a de facto one-person project and the formation of a team was what laid the groundwork for all the successes of the Project that followed. Thus, it has been preserved.

---

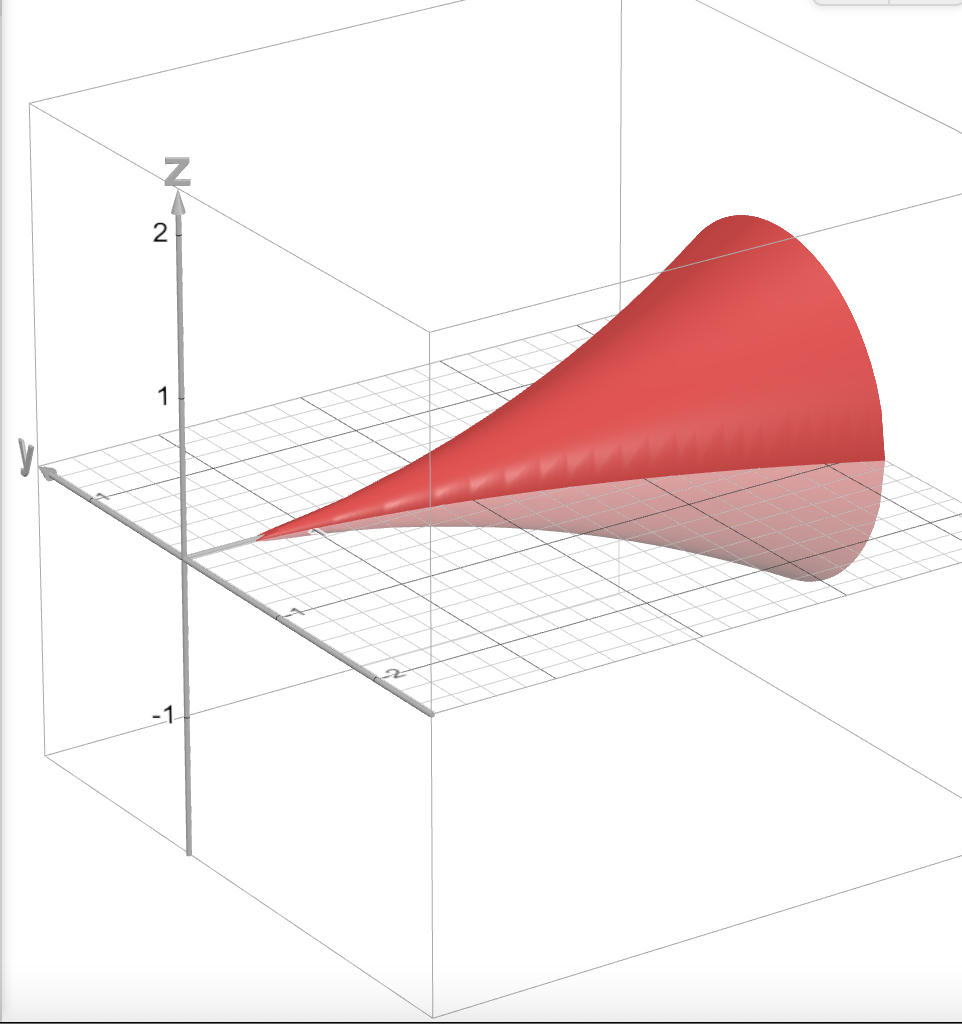
We wish to determine the optimal optical cavity shape to be able to serve as a focuser for a maser beam using the methods of geometric optics. What follows is an (incorrect but interesting) derivation.

Consider a beam of light that makes an angle $\theta$ with the horizontal. Consider that beam hitting a sloped wall with an angle of declination of $\varphi$. Due to Snell’s law, the angle the incoming light beam makes with the wall normal is the same as the angle the outgoing light beam makes with the wall normal:

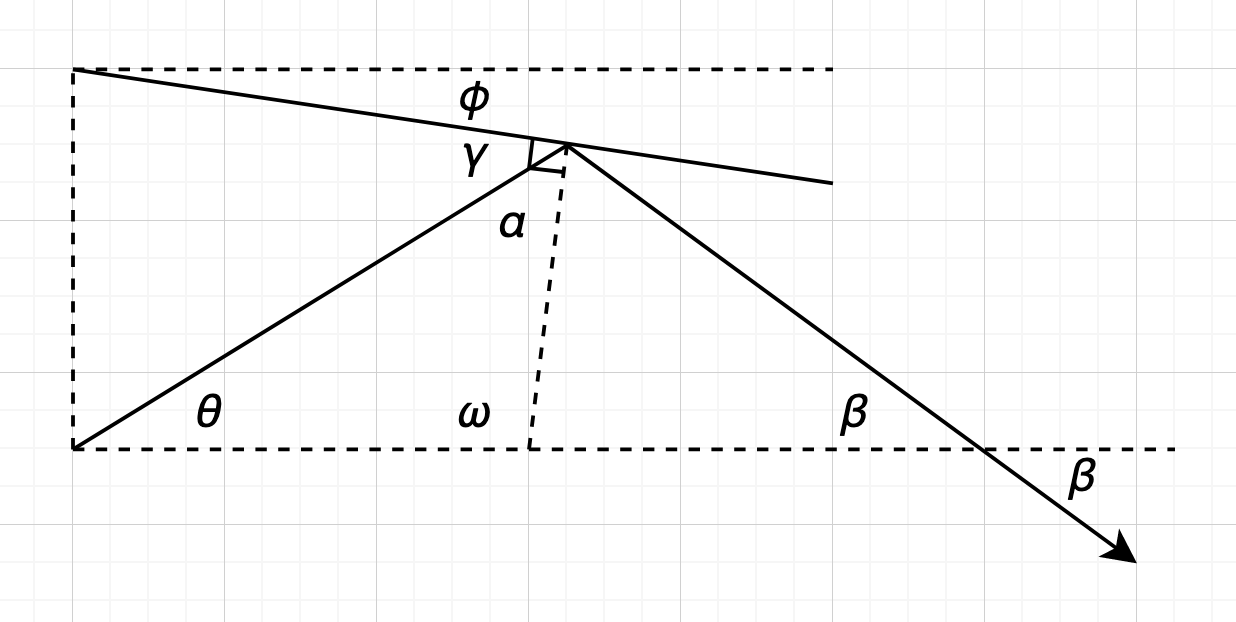
We aim to solve for $\beta$, which is the angle made by the next light beam with the horizontal. To do so, however, we must first calculate the other angles, using the simple geometric fact that $\angle a+\angle b+\angle c=\pi$. First, we calculate $\gamma$:

$$\left(\frac{\pi }{2}-\theta \right)+\gamma +\left(\frac{\pi }{2}-\varphi \right)=\pi$$ $$\gamma =\theta +\varphi$$

Then, we calculate $\alpha$:

$$\alpha =\frac{\pi }{2}-\gamma$$

Then, we calculate $\omega$:

$$\omega +\theta +\alpha =\pi$$ $$\omega =\frac{\pi }{2}+\varphi$$

Finally, we can calculate $\beta$:

$$\beta +\alpha +(\pi -\omega )=\pi$$ $$\beta =\theta +2\varphi$$

We can now say that $\beta ={\theta }_{i+1}$, as it would be the value of $\theta$ for the next bounce, and the whole setup would repeat. From there, we obtain the equation:

$${\theta }_{i+1}={\theta }_i+2{\varphi }_i$$

However, this equation continually increases, whereas what we want is for ${\theta }_n=0$ as we want planar waves. Thus, we add a small correction:

$${\theta }_{i+1}={\theta }_i+2{\varphi }_i$$ $${\varphi }_{i+1}={\varphi }_i-iϵ$$

where $ϵ$ is a suitably small angle. Using this, we find that the resulting curve of $\varphi (x)$ is a curve whose derivative is a straight line, and therefore:

$$f(x)=a{x}^2$$

Using $f(10)=6$ obtained from the equation, we solve for the value $a=\frac{50}{3}$. Therefore, the mathematically ideal surface is a surface of revolution about the x-axis of the curve:

$$f(x)=\frac{3}{50}{x}^2$$