Prototype solar mirror design

In other pages, we have already discussed the importance of the solar mirrors as the primary method of solar energy capture. For more information, see A realistic space-based prototype and Satellite maser engineering.

Construction of a solar mirror

Solar mirrors are not as difficult to construct as may first seem; in many regions, they are used as solar cookers, a low-cost and technologically-simple alternative to gas stoves which can nonetheless reach temperatures high enough to serve an oven. However, the difficulty with our particular circumstances is to construct one that has the optimal parabolic shape and high reflectivity, as our purpose is (obviously) not to cook food, but instead, to power an electron gun, which requires much higher precision.

From the Wikipedia article on solar cookers, which are essentially solar mirrors used for cooking.

A suitable method of assembly is to use sheets of metallized Mylar (which has a very high reflectivity of up to 98%), and then cut it into triangles that we can then arrange into a parabolic dish, as shown:

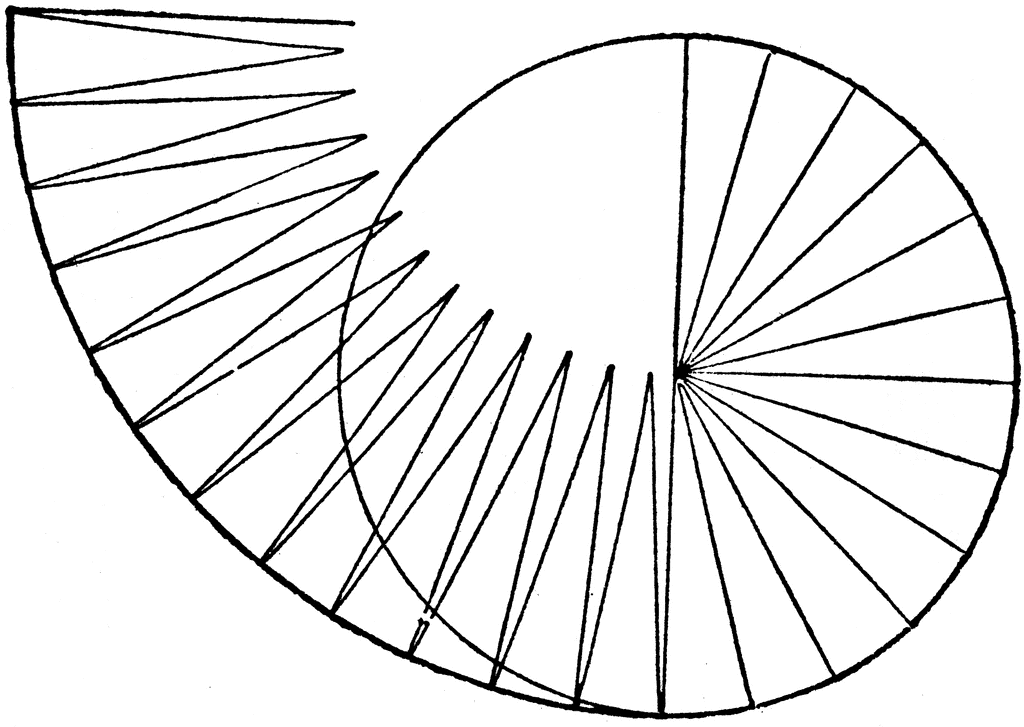
The dish will need to be mounted on a wire-mesh or 3D printed frame, designed carefully to make sure that it has the correct parabolic shape. We may also need clear protective paint to add on top of the Mylar to make it dust-resistant, although that will depend on experimental results.

Mathematical analysis

Assuming that the parabolic dish is an idealized paraboloid, its focus length $f$ is related to its diameter $D=\frac{R}{2}$ (where $R$ is the radius) and depth $d$ (also called the sagitta) by¹:

$$f=\frac{D^2}{16d}=\frac{R^2}{4d}$$

The surface area of the dish is thus given by:

$$S=\frac{\pi R}{6d^2}[(R^2+4d^2{)}^{3/2}-R^3]$$

Assuming that $d$ is small or $R$ is large (or both), the surface area can be well-approximated by a circle of the same radius:

$$S\approx \pi R^2,d/R\ll 1$$

We now consider an aperture placed at the focus of the dish, which is where the concentrated sunlight will enter the electron gun in our design. By straightforward calculations², we can then combine the formula for the total surface area $S$ of the dish (where we can use the approximate form), the value of the solar constant, and the Stefan-Boltzmann law to calculate the maximum temperature that concentrated sunlight can heat a target object to, given by:

$$T={\left(\frac{S{I}_{\odot }}{\pi a^2\epsilon \sigma }\right)}^{1/4}\approx {\left(\frac{I_{\odot }{R}^2}{a^2\epsilon \sigma }\right)}^{1/4}$$

Where ${\sigma }_s=5.67\times 10^{-8}\mathrm{W}\cdot {\mathrm{m}}^2\cdot {\mathrm{K}}^{-4}$ is the Stefan-Boltzmann constant, $S$ is the surface area of the dish, $a$ is the aperture size, $\epsilon$ is the emissivity of the target object, and $I_{\odot }=1361\mathrm{W}/{\mathrm{m}}^2$ is the value of the solar constant. An interactive calculator is available for quickly testing different values of $R$ and $a$, which shows that temperatures in excess of $2000{}^{\circ }\mathrm{C}$ can be obtained, although in practice this is lower due to the effects of atmospheric conditions on the solar constant³, and due to the thermal response of different materials used in thermocathodes.

Footnotes

1. Source: https://www.electronics-notes.com/articles/antennas-propagation/parabolic-reflector-antenna/theory-formulas-equations.php ↩

2. This is assuming an unrealistic ideal case (nearly no atmospheric attenuation, clear skies, and no power loss from the mirror). ↩

3. For more information, see this Wikipedia article. ↩